Build your own Personalized Book Recommendation System

I enjoy reading — but getting good book recommendations that fit my personal interests are hard to get.
However, with user ratings of books publicly available, building a recommender system that can give you personalized book recommendations is actually quite simple.
In this post, I will show you how to build your own personalized book recommender system in Python — from scratch— using a method called collaborative filtering. What you need is a list of 1–5 star ratings of books that you have read.
The Data
To build our own book recommendation system, we need some ratings data of other readers. Here, we will use a dataset called goodbooks-10k, which contains over five million user ratings of the 10.000 most popular books, made publicly available by Goodreads¹.
We can get the dataset by cloning the following repository.
!git clone https://github.com/fkemeth/book_collaborative_filtering.gitThe dataset consists of two files, a book.csv file, which contains the title and author of each book, together with a unique book identifier.
In addition, there is a ratings table, which consists of user ratings ranging from 1–5 stars, together with a unique id for each book and user, respectively.
Let’s import them into pandas dataframes!
import numpy as np
import pandas as pd
books = pd.read_csv("books.csv")[["book_id", "title", "authors"]]
ratings = pd.read_csv("ratings.csv")In order to build a recommender system that can provide us with personalized book recommendations, we need to provide book ratings of our own. In the table below, I list my ratings of books that I have read — replace this list with your 1–5 star ratings of books you have read.
In addition, we need a unique user-id for ourselves — here, I use -1, since all other user-ids are positive.
# Create dataframe with my ratings and a custom user id
my_user_id = -1
my_ratings = [
["The Hitchhiker's Guide to the Galaxy (Hitchhiker's Guide to the Galaxy, #1)", 5],
["The Martian", 5],
["Surely You're Joking, Mr. Feynman!: Adventures of a Curious Character", 5],
['Going Solo', 5],
["Flatland: A Romance of Many Dimensions", 5],
["Gödel, Escher, Bach: An Eternal Golden Braid", 5],
["The Hundred-Year-Old Man Who Climbed Out of the Window and Disappeared", 5],
["Gut: The Inside Story of Our Body’s Most Underrated Organ", 5],
["Brave New World", 4],
["The Three-Body Problem (Remembrance of Earth’s Past, #1)", 2],
["The Dark Forest (Remembrance of Earth’s Past, #2)", 2],
["The Remains of the Day", 5],
["The Pursuit of Happyness", 5],
["Animal Farm", 5],
["1984", 5],
["Norwegian Wood", 5],
["Three Men in a Boat (Three Men, #1)", 5],
["Lord of the Flies", 3],
["Buddenbrooks: The Decline of a Family", 1],
["To Kill a Mockingbird", 5],
["Harry Potter and the Sorcerer's Stone (Harry Potter, #1)", 3],
["Harry Potter and the Chamber of Secrets (Harry Potter, #2)", 3],
["Harry Potter and the Prisoner of Azkaban (Harry Potter, #3)", 3],
["Harry Potter and the Goblet of Fire (Harry Potter, #4)", 3],
["Harry Potter and the Order of the Phoenix (Harry Potter, #5)", 3],
["Harry Potter and the Half-Blood Prince (Harry Potter, #6)", 3],
["Harry Potter and the Deathly Hallows (Harry Potter, #7)", 3],
["Perfume: The Story of a Murderer", 1],
["Sapiens: A Brief History of Humankind", 5],
["The Circle", 1],
["The Reader", 2],
["Cloud Atlas", 5],
["A Briefer History of Time", 5],
["The Grand Design", 4],
["The Universe in a Nutshell", 4],
["All Quiet on the Western Front", 5],
["Inferno (Robert Langdon, #4)", 3],
["The Da Vinci Code (Robert Langdon, #2)", 4],
["I Am Legend", 5],
["Catch Me If You Can: The True Story of a Real Fake", 4],
["Memoirs of a Geisha", 5],
["A Fine Balance", 5],
["Man's Search for Meaning", 5],
["Dune (Dune Chronicles #1)", 4],
["The Kite Runner", 5],
["Kon-Tiki: Across The Pacific In A Raft", 5],
["Seven Years in Tibet", 5],
["The Diary of a Young Girl", 5],
["The Alchemist", 5],
["Siddhartha", 5],
["The Glass Bead Game", 4],
["Demian. Die Geschichte von Emil Sinclairs Jugend", 5],
["Steppenwolf", 4],
["Quo Vadis", 5],
["P.S. I Love You", 4],
["The Pillars of the Earth (The Kingsbridge Series, #1)", 4],
["Eye of the Needle", 4],
["Eragon (The Inheritance Cycle, #1)", 4],
["Wild Swans: Three Daughters of China", 5],
["I Am Malala: The Story of the Girl Who Stood Up for Education and Was Shot by the Taliban", 5]
]
my_ratings = pd.DataFrame(my_ratings, columns=['title', 'rating'])
my_ratings['user_id'] = my_user_id
my_ratings = pd.merge(my_ratings, books, on='title', how='left')
# Append my ratings to the ratings table
ratings = ratings.append(my_ratings[['user_id', 'book_id', 'rating']], ignore_index=True)
ratings = ratings.merge(books[["book_id", "title"]], how="left", on="book_id").dropna()Using Collaborative Filtering for Creating Personalized Book Recommendations
Collaborative filtering is a very simple and widely used method to create personalized recommendations based on data.
Roughly speaking, the method consists of two steps:
- Based on your ratings, calculate how similar all the other users are to you, given their ratings. The simplest way to do this is to calculate the correlation coefficient between your ratings and the ratings of all other users.
- For books you haven’t rated (read) yet, calculate predicted ratings (scores) based on the ratings of the users that are most similar to you. As discussed below, this can be done by averaging the ratings of those most similar users.
Since it is based on similarities between users, this method is also called user-user collaborative filtering².
To illustrate how user-user collaborative filtering works, imagine the ratings in the table below. On the left, we have the actual ratings of four users, whereby user 3 has not rated (read) book B yet. If we want to predict the rating of user 3 on book B, we search for users that provided similar ratings on books that user 3 has rated as well. In this example, user 1 gave the same ratings as user 3 except on book A, where she gave 4 instead of 5 stars, and similarly user 4 gave the same ratings except on book C, with 1 instead of two stars. In contrast, user 2 did not agree on any book with user 3.
So in order to provide a prediction on book B for user 3, user-user collaborative filtering would average the ratings of the most similar users (also called neighbors, here users 1 and 4), which yields a predicted rating of 5 for book B.
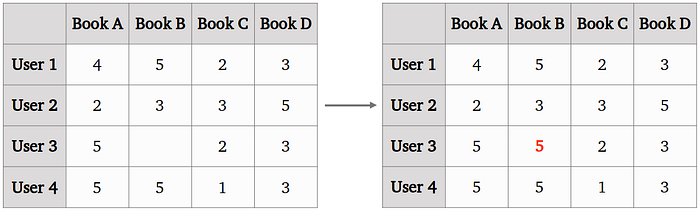
1. User Similarities
In order to calculate similarities between the users, we write our original ratings table from above as a so-called user-item-interaction matrix, whereby each row corresponds to a user and each column corresponds to a book title (as in the toy example we just discussed).
Since there are thousands of books, this matrix will be very sparse, with mostly NaN values (empty cells) except in places where we actually have a rating of a user for a particular book!
uii_matrix = ratings.pivot_table(
index=["user_id"],
columns=["title"],
values="rating").fillna(np.nan)For calculating the similarity to all users, we calculate the correlation coefficients between our ratings (the row in the user-item interaction matrix corresponding to our id) and all other rows. Notice that each user is represented by their ratings only! In particular, if a user gave the same ratings as we did on all books we have rated, the correlation between that user and us will be maximal, and the correlation coefficient will be 1. In contrast, if another user rated all books with 1 star that we have rated with 5 stars, the correlation coefficient will be small. For calculating the correlation coefficients, we can use the pre-built function corrwith from pandas.
similarities = uii_matrix.corrwith(uii_matrix.loc[my_user_id], axis=1)Note that there will be many users that have only rated one or a few books of the books we have rated. If those users gave the same ratings as we did on those books that we have in common, they will get a correlation coefficient of 1. However, we can not really be sure that they have similar tastes in books as we do, since we have only those few ratings as evidence. A common trick is to require a minimum number of commonly-rated books to consider another user as a similar user. We therefore remove all users that have read less than 10 books that we have rated.
minimum_number_of_books_rated_in_common = 10
# Only use those which have an intersection of more than n books
my_books_read = uii_matrix.loc[my_user_id].notna()
intersections = uii_matrix.apply(lambda x: (x.notna() & my_books_read).sum(), axis=1)
similarities[intersections < minimum_number_of_books_rated_in_common] = np.nan
# Remove self similarity
similarities[my_user_id] = np.nan2. Scoring
Having calculated how similar each user is to us, we can predict now a rating for each book that we have not read yet. For each of those books, collaborative filtering averages the ratings of similar users that have rated those books. That is, if similar users gave 5 stars to a book that we haven’t read yet, we assume that chances are high that we would like this book as well.
What similar user means is again a bit arbitrary — here, we use a threshold of 0.7, considering all users similar (as neighbors) that have a correlation coefficient of 0.7 or higher.
Instead of simply averaging the ratings of those similar users, collaborative filtering uses a weighted average of the ratings, weighted by the similarity (the correlation coefficient) between the users and us.
Finally, we again want to have some statistics on the ratings for us to trust them. That is, if we have just one rating of a similar user for a book we did not read yet, we might put less trust in that rating than if it would have been rated by 10 similar users. We therefore neglect all books that have only been rated 5 or fewer times by similar users.
That’s it, with that, we can calculate predicted ratings for all books, and print out those books with the highest predicted ratings!
minimal_similarity = 0.7
minimal_number_of_ratings = 5
def scoring(column):
# Consider those users with at least a similarity of minimal_similarity
neighbours = similarities > minimal_similarity
# Calculate weighted mean of ratings as scores
numerator = np.sum(column[neighbours]*similarities[neighbours])
denominator = np.sum(similarities[neighbours][column[neighbours].notna()])
predicted_rating = numerator/denominator if denominator != 0 else np.nan
# If book has been rated less than minimal_number_of_ratings, set its score to nan
if column[neighbours].notna().sum() <= minimal_number_of_ratings:
predicted_rating = np.nan
return predicted_rating
scores = uii_matrix.apply(lambda x: scoring(x))
# Print only recommendations of books I haven't read:
print(scores[~my_books_read].sort_values(ascending=False)[:10])Below are the top-10 personalized book recommendations with scores:
I built this book recommender over a year ago, and got quite interesting book recommendations — in particular of books from authors I did not know before. However there are a few pro and cons of this approach that should be highlighted
Pros
- Collaborative filtering is quite simple and intuitive — based on ratings, we look for users that are similar to use, and use the average of their ratings as predictions.
- The predicted ratings are explainable — we can check on which users they are based, and what other books those users rated.
Cons
- The predictions strongly depend on hyperparameters. Without using a proper evaluation framework, it is difficult to estimate good values for the minimal similarity, the minimal number of ratings, and the minimal number of commonly-rated books that we used above.
- Different users have different rating-scales — that is, some users tend to rate more in the 3–5 star range, others more in the 1–4 star range. Normalizing their ratings using their respective mean rating does usually improve the recommendations
- The user-item interaction matrix is quite large — it therefore requires some memory, and calculating the similarities to all users takes some time.
- Since the method is based on user ratings only, it requires to input a decent number of ratings — when I used 20 ratings or fewer I did not get very good book recommendations.
- In the user-user collaborative filtering, as we used it here, we need to compute the similarities between ourselves and all users — this can be very expensive if the number of users in the dataset is large. An alternative is to use item-item collaborative filering³.
- The approach is not time-sensitive. If you give 5-star ratings to books that you enjoyed when you were younger, but would not enjoy reading now, chances are high you will get recommendations of books that you might have enjoyed back then, but are not really relevant for you anymore now.
The scikit-surprise package⁴ has many recommendation system approaches already implemented — instead of writing the collaborative filtering algorithm from scratch, as we did, you can use their kNN implementation.
You can find the code here:
https://github.com/fkemeth/book_collaborative_filtering
Thank you for reading!
References
[1] Data: goodbooks-10k, https://github.com/zygmuntz/goodbooks-10k
[2] J.B. Schafer, D. Frankowski, J. Herlocker, S. Sen: Collaborative filtering recommender systems, https://doi.org/10.1145/3130348.3130372
[3] B. Sarwar, G. Karypis, J. Konstan, J. Riedl, Item-based collaborative filtering recommendation algorithms, https://dl.acm.org/doi/10.1145/371920.372071
[4] https://surpriselib.com/
